图论进阶

发表于 更新于 分类于 阅读次数： Changyan：

图论进阶

差分约束

1.可以用来求一个不等式组的可行解

2.可以求最大值或者最小值

对于每一个不等式

我们可以借助最短路模型中的三角不等式

j 和 i 对应两个点，之间的长度对应常数c.

因此借助此性质建图，我们只需任取超级源点（此源点出发要能遍历所有边，因此考虑超级源点）进行遍历，得到的每一个点到起点的最短路径即为对应可行解。

总结:

[1]先将每一个不等式转化为从xj走到xi,长度为c的一条边

[2]找一个超级源点使得该点能够遍历到所有边

[3]从源点求一遍单源最短路

[4]对于形如xi<=c的转化方式：建立一个虚拟源点，等价于

结果：

[1]如果存在负环，原不等式组一定无解

[2]如果没有负环，则 dist[i]就是原不等式组的一个解

求最大可行解与最小可行解

结论1：如果求的是最小值，则应该使用最长路(ge)

结论2：如果求的是最大值，则应该使用最短路(le)

结论2证明：倘若求Xi的最大值，即求出Xi的所有上界取最小值，即等于最短路径的长度,使用≤号来规范

小技巧：如果发现超时了有两种Debug技巧

1.检查数组是不是开小了

2.将SPFA中的队列改成栈

3.记住，一定是从小的向大的连边，以大于为例，a>=b+c表示从b向a连一条长度为c的边（最长路）a<=b+c表示从b向a连一条长度为c的边（最短路）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
bool spfa(){
    int res=0;
    memset(dist,-0x3f,sizeof dist);
    dist[0]=0;

    stack<int> Q;
    Q.push(0);

    while(Q.size()){
        int t=Q.top();
        Q.pop();
        st[t]=false;

        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(dist[j]<dist[t]+w[i]){
                dist[j]=dist[t]+w[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>n) return false;
                if(!st[j]){
                    Q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    return true;
}

对于差分约束有三种做法：

1
2
3
4
以求最长路为例：
[1]边权无限制	SPFA	O(km~nm)
[2]边权非负		Tarjan
[3]边权为正		拓扑序计算最长路

最近公共祖先LCA

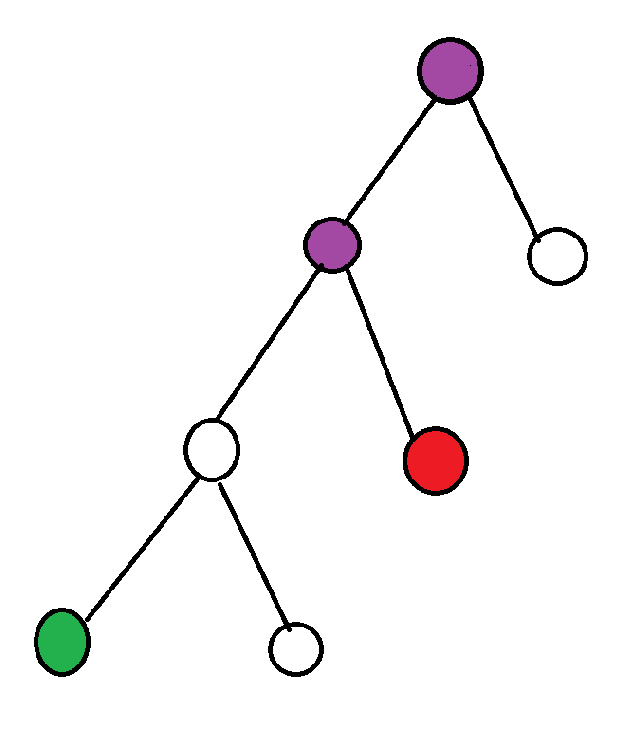
对于一棵树：

绿色的点都是⭐的祖先

当一个点同时是另外两个点的祖先时，成为这两点的公共祖先

紫色点是绿色与红色点的公共祖先

求法：

1.向上标记法

从某一个点向上遍历并标记。再从另外一个点开始标记，标记到的第一个已经被标记到的点便是最近公共祖先

2.树上倍增LCA

倍增f[i,j]表示从i开始，向上走2^j所能走到的所有节点

预处理,一般使用BFS

fa[i,j]表示从i开始，向上走2^j步所能走到的节点。0<=j<=logn

depth[i]表示深度

哨兵：如果从i开始跳2^j步会跳过根节点，那么fa[i,j]=0.depth[0]=0

在线step:

[1]先将两个点跳到同一层

[2]判断a与b之间的关系

[3]让两个点同时往上跳，一直跳到他们最近公共祖先的下一层。

跳法：从最大的二的整次幂开始跳

预处理O(nlogn)

查询O(logn)

板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
void bfs(int root){
    depth[0]=0,depth[root]=1;  //depth[0]初始化深度为0表示不合法的深度
    queue<int> Q;Q.push(root);
    
    while(Q.size()){
        int t=Q.front();
        Q.pop();
        
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(depth[j]>depth[t]+1){
                depth[j]=depth[t]+1;
                
                Q.push(j);
                fa[j][0]=t;
                for(int k=1;k<=15;k++)
                    fa[j][k]=fa[fa[j][k-1]][k-1];
            }
        }
    }
}

inline int lca(int a,int b){
    if(depth[a]<depth[b]) swap(a,b);
    //从后向前遍历
    for(int i=15;i>=0;i--){
        if(depth[fa[a][i]]>=depth[b]) 
            a=fa[a][i];
    }
    
    if(a==b) return a;
    
    for(int i=15;i>=0;i--)
        if(fa[a][i]!=fa[b][i]){
            a=fa[a][i],b=fa[b][i];
        }
    return fa[a][0];
}

Tarjan缩点———离线求LCA O(n+m)

对向上标记法的优化，基于DFS

DFS的过程中将点分成三类：

其中，绿色部分为已经被遍历且回溯的2类点，红色为正在遍历的1号点。对于每一个1号点与2号点的组合，他们的最近公共祖先一定在1号点的父辈节点上，因此可以考虑使用并查集将2类点压缩到1类点的路径上。

如果求2区域内的点与x的最近公共祖先，可以将绿颜色部分（已经遍历且回溯过的点）合并到1区域的根节点上（使用并查集维护）

1
2
3
4
5
6
7
8
tarjan缩点step:
	[1]预处理步骤，存储所有询问，保存数组中时应该保存并双向，dfs出所有的点距
tarjan:
	[2]类似于深度搜索，标记当前点为第1类点（如上图红）
    遍历所有以当前点为根节点的点，如果未被标记则搜索，然后并查集合并
	[3]对于与当前点有关的询问，如果另外一个点被标记为图上绿（已遍历且回溯）
    则计算出距离并记录答案。
    [4]当前点已经被遍历且回溯，应当标记为第二类点

附上板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void dfs(int u,int father){ //算出每个点到根节点的距离
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(j==father) continue;
        dist[j]=dist[u]+w[i];
        dfs(j,u);
    }
}

void tarjan(int u){
    st[u]=1;
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(!st[j]){
            tarjan(j);
            fa[j]=u;
        }    
    }
    
    for(int i=0;i<query[u].size();i++){
        int ver=query[u][i].x,id=query[u][i].y;
        if(st[ver]==2){ //如果已经被划分到了左边被遍历过的子树中
            int root=find(ver);
            res[id]=dist[u]+dist[ver]-2*dist[root];
        }
    }
    st[u]=2;
}
RMQ+DFS序

1
2
3
4
[1]深度优先搜索出这一颗树的dfs序（根节点出现多次）
[2]求节点x和节点y之间的最近公共祖先，
   即在dfs序中任意x,y之间找最小值
[3]找区间最小值可以使用RMQ算法

树上差分：

最近公共祖先减少2，两个节点各增加1

1
2
3
cnt[root]-=2;
cnt[a]++;
cnt[b]++;

有向图的强连通分量SCC

  • 关于图上的传递性

定义：对于一个有向图，连通分量中的任意两点u，v；必有可以从u走到v，也可以从v走到u

强连通分量：极大连通分量，即不能再增加点使得其仍然是一个连通分量

作用：将一个有向图缩点成有向无环图(DAG)

1
2
3
4
5
将点分为4类：
    [1]树枝边  (x,y)
    [2]前向边  (a,b)
    [3]后向边  (m,n)
    [4]横叉边  (b,y)

问题：某一点是否在强连通分量中？

  • 情况1：存在后向边指向祖先节点
  • 情况2：先到横叉边，横叉边再通过后向边走到祖宗节点

step：

1
2
3
4
5
Tarjan算法求强连通分量(SCC)
对每个点定义两个时间戳
[1]dfn[u]表示遍历到u的时间戳
[2]low[u]表示从u开始走所能遍历到的最小的时间戳
[3]u是其所在的强连通分量的最高点，等价于dfn[u]=low[u]

Tarjan_scc模板 O(n+m)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void tarjan(int u){
    int top=0;
    dfs[u]=low[u]=++timestamp;
    stk[++top]=u,in_stk[u]=true;
    
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(!dfn[j]){
            tarjan(j);
            low[u]=min(low[u],low[j]);    //u能到j，j能到的最小值u也一定能到
        }
        else if(in_stk[j]){     //栈中存储的所有点都不是其所在的强连通分量的最高点
            low[u]=min(low[u],dfn[j]);     //此时的j要么是祖先，要么是横叉点
        }
 	}
  	if(dfn[u]==low[u]){   //找到了强连通分量的最高点
    	int y;
        scc_cnt++;
        do{
       	    y=stk[top--];
            in_stk[y]=false;
            id[y]=scc_cnt;                                
        } while(y!=u);
    }
}

紧接着需要做缩点操作，用来建新图（DAG）：

1
2
3
4
5
6
7
//缩点
for(int dot=1;dot<=n;dot++)
    for(int i=h[dot];~i;i=ne[i]){
        int j=e[i];
        if(id[i]!=id[j])  //如果i和j不在一个强连通分量中
            add(id[i],id[j]); //在两个强连通分量之间加一条边(建图）
    }

连通分量在缩完点之后就已经是满足拓扑序了，因此可以不用再写拓扑排序

性质：1）将一个有向图转化为强连通分量所需要加的边的最小个数为

无向图的双连通分量（无向图）

无向图有两种双连通分量

  • 第一种是边的双连通分量
  • 第二种是点的双连通分量

e-DCC 边的双连通分量

桥：是一个无向边。对于一个无向连通图，如果删除某一条边便会变得不连通，那么称这条边为桥

定义：极大的，不含有桥的连通区域被称为边的双连通分量

性质：[1]删去任意一条边仍然是连通图

​ [2]任意两点之间一定包含两条不相交的路径

​ [3]将一个无向图转化为边的双连通分量最小需要加的边的个数是

无向图中存在类似于有向图中的三种边：

1
2
3
[1]树枝边  (x,y)
[2]前向边  (a,b)
[3]后向边  (m,n)

方法:

1
2
3
4
5
6
7
[1]类似于SCC，首先引入时间戳预处理出：
    dfn[x]:遍历到x节点的时间戳
    low[x]:x所能遍历到的最小的时间戳
[2]找到桥<=>找到dfn[x]<low[y]  //y在x下方，y无论如何也走不到x
[3]找到所有边的连通分量有两种方法：
    1)将所有桥删除掉，剩下的每一个连通块都是一个连通分量
    2)类似于有向图，借助stack来判断dfn[x]==low[x]

step：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void tarjan(int u,int from){
    dfn[u]=low[u]=++timestamp;
    stk[++top]=u;
    
    for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(!dfn[j]){
            tarjan(j,i);  //from是反向边，此处为i
            low[u]=min(low[u],low[j]);
            
            if(dfn[u]<low[j]){   //如果满足桥的性质
                is_bridge[i]=is_bridge[i^1]=true;  //加边的时候是一偶一奇加的
            }
        }
        else if(i!=(from^1))  //如果不是反向边
            low[u]=min(low[u],dfn[j]);
    }
    
    if(dfn[u]==low[u]){  //找到了一个dcc
        dcc_cnt++;
        int y;
        do{
            y=stk[top--];
            id[y]=dcc_cnt;
        }while(y!=u);
    }
}

v-DCC点的双连通分量

割点：在一个无向图中如果删去某一个点使得整个图变得不连通，则称此点为此无向图的割点

定义：极大的，不包含个点的连通块被称为点的双连通分量

性质：每一个割点至少属于两个连通分量

1
2
3
4
求割点：
    [1]满足low[y]>=dfn[x]后需要分类讨论
    [2]如果x不是根节点，那么x是割点
    [3]如果x是根节点，则其至少有两个子节点yi都满足low[yi]>=dfn[x],此时x才能算割点

求点的双连通分量思路：

1
2
3
4
5
6
7
8
9
10
[1]记录时间戳，当前点入栈
[2]特判,如果是孤立点就单独记录进对应连通块的数组
[3]遍历所有邻边，并更新。如果没有更新过
    当找到了dfn[x]<=dfn[y]之后要对其讨论是否是割点:
        if(dfn[x]<=low[y]){
            cnt++;//对于记录当前有多少个分支+1  
            if(x!=root||cnt>1) x是割点
            将栈中元素弹出直至弹出y为止
            将x也放入当前双连通分量中
        }

二分图

二分图算法

1
2
3
4
5
6
7
8
9
10
11
12
13
二分图{//一个图是二分图当且仅当图中不含奇数环
	1.染色法{ O(n+m)
		1.建邻接表
		2.for(1~n)
			if(i未染色）
				dfs(i)
		需要标记每个点是否被染色
	}
	关键的bool dfs:
		1.标记颜色
		2.遍历此点所有连接的点，如果没有被染色，则染色并dfs,若返回false 则返回false（这里的迭代十分关键，看代码）
		3.否则如果染过颜色，则判断颜色是都矛盾
		4.都没问题返回true

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool dfs(int x,int k){
    color[x]=k;
    for(int i=h[x];i!=-1;i=ne[i]){
        int j=e[i];
        if(!color[j]){
            if(!dfs(j,3-k)) return false;
        }
        else if(color[j]==k) return false;
    }
    return true;
}
//之后的main函数内：
for(int i=1;i<=n;i++){
    if(!color[i]){
        if(!dfs(i,1)){
            flag=false;
            break;
        }
    }
}
if(!flag) puts("No");
else puts("Yes");

匈牙利算法

在使用匈牙利算法之前一定要证明是二分图，即可以二染色！
遍历二分图要找的点每一个对应点
如果此点不在配对成功的集合中{
    将此点加入配对成功的集合
    如果此映射点没有被配对或者将其配对的点有其他可配对的点，则返回配对成功(对应函数外侧更新答案)
}

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
bool find(int x){
    for(int i=h[x];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[j]){
            st[j]=true;
            if(match[j]==0||find(match[j])){
                match[j]=x;
                return true;
            }
        }
    }
    return false;
}

1.二分图不存在奇数换，染色法不存在矛盾问题

2.匈牙利算法，匹配，最大匹配，匹配点，增广路经

1
2
3
4
匹配：即没有公共点的边
最大匹配：边数最多的匹配
匹配点：在匹配中的点
增广路径：从一个非匹配点走，依次走非匹配边与匹配边，直到通过非匹配边走到一个非匹配点

结论：

3.最小点覆盖，最大独立集，最小路径点覆盖，最小路径重复点覆盖

最大匹配数=最小点覆盖=总点数-最大独立集=总点数-最小路径覆盖

1
最小点覆盖:从一个图中选出最少的点使得使得每一条边至少有一个端点被选出来
1
2
3
4
5
6
7
8
9
10
11
12
13
证明:最小点覆盖数=最大匹配数      
[1]最小点覆盖数>=最大匹配数：
	每一条边都选出一个点即可
[2]最小覆盖数与最大匹配数之间可取等号：
将一个图分成两半，构造：
	从左边每个非匹配点做一遍匈牙利算法，并标记所有经过的点。最终选出左边未被标记的点和右边被标记的点

上述构造满足三个性质：
    1)左边所有未被标记的点都是匹配点
    2)右边所有被标记的点都是匹配点
    3)对于匹配边，要么左右全被标记，要么全不被标记

因此选出来的点恰好可以满足最小覆盖，因为每个匹配边有且只有一个点被选

  • 最大独立集：从一个图中选出最多的点使得选出的点之间无边<=>去掉最少的点将所有边都破坏掉

  • 最大团：选出最大的点使得任意两点之间都有边

  • 最小路径点覆盖：在DAG中用最少的互不相交的路径（从起点连连连到终点）将所有点覆盖，拆点将每个点分成出点和入点，使得原图变成一个二分图
  • 最小路径重复点覆盖:
    • [1]求传递闭包(如果一个点间接连向另外一个点的话就直接加一条边)得到G’
    • [2]在G’上求最小路径覆盖

4.最优匹配 KM算法/最小费用流

5.多重匹配（多夫多妻）最大流

欧拉路径与欧拉回路问题

大前提所有点都是连通的

欧拉路径：
  • 是否存在一条路径每个边之走一遍

对于无向图：

  • 欧拉路径（一笔画）问题的解决方案：所有奇数路径的点（奇点）的个数只能是0或者2个。如果是2个只能位于起点或者终点

对于有向图：

  • 欧拉路径
    • [1]所有点的入度等于出度
    • [2]除了起点和终点之外的所有点的出度等于入度。起点的出度比入度多1，终点的入度比出度多1
欧拉回路：
  • 是否存在一个环路，每个边恰好走一次之后又回到原来的地方

对于无向图

  • 欧拉回路的度数为奇数的点只能由0个

对于有向图

  • 所有的点出度等于入度

算法：

1
2
3
4
5
6
7
8
dfs(int u){
	for(int i=h[u];~i;i=ne[i]){
        int j=e[i];
        if(!st[j])
        	dfs(i);
    }
    queue.push(u);
}

如果是有向图，则使用之后删去此边

如果是无向图，经过一条边之后应该标记反向边，标记方法&1（因为加入的时候是01，23..加入的）

板子：(优化)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void dfs(int u){
    for(int &i=h[u];~i;){
        if(st[i]){   //如果已经标记过来就直接删除
            i=ne[i];
            continue;
        } 
        st[i]=true;  //标记当前边
        if(T==1) st[i^1]=true;  //如果是无向图就加双向边
        
        int t;
        //先算出要加的边
        if(T==1){
            t=i/2+1;
            if(i&1) t=-t;
        }
        else t=i+1;
        //先把当前边删除再遍历，这样能保证每个边只被遍历依次
        int j=e[i];
        i=ne[i];
        dfs(j);
        Q.push(t);
        
    }
}

或者

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void dfs(int u)
{
    while(~h[u])
    {
        int i = h[u];
        if(used[i]) {
            h[u] = ne[i];
            continue;
        }

        h[u] = ne[i];
        used[i] = true;
        if(type == 1) used[i ^ 1] = true;

        dfs(e[i]);
        if(type == 1) {
            int t = i / 2 + 1;
            if(i & 1) t *= -1;
            ans[ ++ cnt] = t;
        }
        else ans[ ++ cnt] = i + 1;
    }
}